%install '.package(path: "$cwd/FastaiNotebook_06_cuda")' FastaiNotebook_06_cuda
Installing packages: .package(path: "/home/ubuntu/fastai_docs/dev_swift/FastaiNotebook_06_cuda") FastaiNotebook_06_cuda With SwiftPM flags: [] Working in: /tmp/tmplakka2c8 Fetching https://github.com/mxcl/Path.swift Fetching https://github.com/JustHTTP/Just Completed resolution in 3.11s Cloning https://github.com/JustHTTP/Just Resolving https://github.com/JustHTTP/Just at 0.7.1 Cloning https://github.com/mxcl/Path.swift Resolving https://github.com/mxcl/Path.swift at 0.16.2 Compile Swift Module 'Just' (1 sources) Compile Swift Module 'Path' (9 sources) Compile Swift Module 'FastaiNotebook_06_cuda' (10 sources) Compile Swift Module 'jupyterInstalledPackages' (1 sources) Linking ./.build/x86_64-unknown-linux/debug/libjupyterInstalledPackages.so Initializing Swift... Loading library... Installation complete!
Load data¶
import FastaiNotebook_06_cuda
%include "EnableIPythonDisplay.swift"
IPythonDisplay.shell.enable_matplotlib("inline")
('inline', 'module://ipykernel.pylab.backend_inline')
// export
import Path
import TensorFlow
import Python
let plt = Python.import("matplotlib.pyplot")
let data = mnistDataBunch(flat: false, bs: 512)
let opt = SGD<CnnModel, Float>(learningRate: 0.4)
func modelInit() -> CnnModel { return CnnModel(sizeIn:28, channelIn: 1, channelOut: 10, nFilters: [8, 16, 32, 32]) }
let learner = Learner(data: data, lossFunction: softmaxCrossEntropy, optimizer: opt, initializingWith: modelInit)
let recorder = learner.makeDefaultDelegates(metrics: [accuracy])
learner.delegates.append(learner.makeNormalize(mean: mnistStats.mean, std: mnistStats.std))
time { try! learner.fit(1) }
Epoch 0: [0.3132431, 0.9025] 25091.188661 ms
Batchnorm¶
Custom¶
Let's start by building our own BatchNorm layer from scratch. Eventually we intend for this code to do the trick:
struct AlmostBatchNorm<Scalar: TensorFlowFloatingPoint>: Differentiable {
// Configuration hyperparameters
@noDerivative let momentum: Scalar
@noDerivative let epsilon: Scalar
// Running statistics
@noDerivative var runningMean: Tensor<Scalar>
@noDerivative var runningVariance: Tensor<Scalar>
// Trainable parameters
var scale: Tensor<Scalar>
var offset: Tensor<Scalar>
init(featureCount: Int, momentum: Scalar = 0.9, epsilon: Scalar = 1e-5) {
self.momentum = momentum
self.epsilon = epsilon
self.scale = Tensor(ones: [Int32(featureCount)])
self.offset = Tensor(zeros: [Int32(featureCount)])
self.runningMean = Tensor(0)
self.runningVariance = Tensor(1)
}
mutating func applied(to input: Tensor<Scalar>, in context: Context) -> Tensor<Scalar> {
let mean: Tensor<Scalar>
let variance: Tensor<Scalar>
switch context.learningPhase {
case .training:
mean = input.mean(alongAxes: [0, 1, 2])
variance = input.variance(alongAxes: [0, 1, 2])
runningMean += (mean - runningMean) * (1 - momentum)
runningVariance += (variance - runningVariance) * (1 - momentum)
case .inference:
mean = runningMean
variance = runningVariance
}
let normalizer = rsqrt(variance + epsilon) * scale
return (input - mean) * normalizer + offset
}
}
But there are some automatic differentiation limitations (control flow support) and Layer protocol constraints (mutating applied) that make this impossible for now (note the lack of @differentiable or a Layer conformance), so we'll need a few workarounds. A Reference will let us update running statistics without declaring the applied method mutating:
//export
class Reference<T> {
var value: T
init(_ value: T) {
self.value = value
}
}
The following snippet will let us differentiate a layer's applied method if it's composed of training and inference implementations that are each differentiable:
//export
protocol LearningPhaseDependent: Layer {
@differentiable func applyingTraining(to input: Input) -> Output
@differentiable func applyingInference(to input: Input) -> Output
}
extension LearningPhaseDependent {
func applied(to input: Input, in context: Context) -> Output {
switch context.learningPhase {
case .training: return applyingTraining(to: input)
case .inference: return applyingInference(to: input)
}
}
@differentiating(applied)
func gradApplied(to input: Input, in context: Context) ->
(value: Output, pullback: (Output.CotangentVector) ->
(Self.CotangentVector, Input.CotangentVector)) {
switch context.learningPhase {
case .training:
return valueWithPullback(at: input) {
$0.applyingTraining(to: $1)
}
case .inference:
return valueWithPullback(at: input) {
$0.applyingInference(to: $1)
}
}
}
}
Now we can implement a BatchNorm that we can use in our models:
//export
protocol Norm: Layer {
associatedtype Scalar
typealias Input = Tensor<Scalar>
typealias Output = Tensor<Scalar>
init(featureCount: Int, epsilon: Scalar)
}
struct FABatchNorm<Scalar: TensorFlowFloatingPoint>: LearningPhaseDependent, Norm {
// Configuration hyperparameters
@noDerivative let momentum: Scalar
@noDerivative let epsilon: Scalar
// Running statistics
@noDerivative let runningMean: Reference<Tensor<Scalar>>
@noDerivative let runningVariance: Reference<Tensor<Scalar>>
// Trainable parameters
var scale: Tensor<Scalar>
var offset: Tensor<Scalar>
// TODO: check why these aren't being synthesized
typealias Input = Tensor<Scalar>
typealias Output = Tensor<Scalar>
init(featureCount: Int, momentum: Scalar, epsilon: Scalar = 1e-5) {
self.momentum = momentum
self.epsilon = epsilon
self.scale = Tensor(ones: [Int32(featureCount)])
self.offset = Tensor(zeros: [Int32(featureCount)])
self.runningMean = Reference(Tensor(0))
self.runningVariance = Reference(Tensor(1))
}
init(featureCount: Int, epsilon: Scalar = 1e-5) {
self.init(featureCount: featureCount, momentum: 0.9, epsilon: epsilon)
}
@differentiable
func applyingTraining(to input: Tensor<Scalar>) -> Tensor<Scalar> {
let mean = input.mean(alongAxes: [0, 1, 2])
let variance = input.variance(alongAxes: [0, 1, 2])
runningMean.value += (mean - runningMean.value) * (1 - momentum)
runningVariance.value += (variance - runningVariance.value) * (1 - momentum)
let normalizer = rsqrt(variance + epsilon) * scale
return (input - mean) * normalizer + offset
}
@differentiable
func applyingInference(to input: Tensor<Scalar>) -> Tensor<Scalar> {
let mean = runningMean.value
let variance = runningVariance.value
let normalizer = rsqrt(variance + epsilon) * scale
return (input - mean) * normalizer + offset
}
}
//export
struct ConvBN<Scalar: TensorFlowFloatingPoint>: Layer {
var conv: Conv2D<Scalar>
var norm: FABatchNorm<Scalar>
init(
filterShape: (Int, Int, Int, Int),
strides: (Int, Int) = (1, 1),
padding: Padding = .valid,
activation: @escaping Conv2D<Scalar>.Activation = identity
) {
// TODO (when control flow AD works): use Conv2D without bias
self.conv = Conv2D(
filterShape: filterShape,
strides: strides,
padding: padding,
activation: activation)
self.norm = FABatchNorm(featureCount: filterShape.3, epsilon: 1e-5)
}
@differentiable
func applied(to input: Tensor<Scalar>, in context: Context) -> Tensor<Scalar> {
return norm.applied(to: conv.applied(to: input, in: context), in: context)
}
}
// Would be great if this generic could work
// struct ConvNorm<NormType: Norm, Scalar: TensorFlowFloatingPoint>: Layer
// where NormType.Scalar == Scalar {
// var conv: Conv2D<Scalar>
// var norm: NormType
// init(
// filterShape: (Int, Int, Int, Int),
// strides: (Int, Int) = (1, 1),
// padding: Padding = .valid,
// activation: @escaping Conv2D<Scalar>.Activation = identity
// ) {
// // TODO (when control flow AD works): use Conv2D without bias
// self.conv = Conv2D(
// filterShape: filterShape,
// strides: strides,
// padding: padding,
// activation: activation)
// self.norm = NormType.init(featureCount: filterShape.3, epsilon: 1e-5)
// }
// @differentiable
// func applied(to input: Tensor<Scalar>, in context: Context) -> Tensor<Scalar> {
// return norm.applied(to: conv.applied(to: input, in: context), in: context)
// }
// }
//typealias ConvBN = ConvNorm<BatchNorm<Float>, Float>
//export
struct CnnModelBN: Layer {
var reshapeToSquare = Reshape<Float>([-1, 28, 28, 1])
var conv1 = ConvBN<Float>(
filterShape: (5, 5, 1, 8),
strides: (2, 2),
padding: .same,
activation: relu)
var conv2 = ConvBN<Float>(
filterShape: (3, 3, 8, 16),
strides: (2, 2),
padding: .same,
activation: relu)
var conv3 = ConvBN<Float>(
filterShape: (3, 3, 16, 32),
strides: (2, 2),
padding: .same,
activation: relu)
var conv4 = ConvBN<Float>(
filterShape: (3, 3, 32, 32),
strides: (2, 2),
padding: .same,
activation: relu)
var pool = AvgPool2D<Float>(poolSize: (2, 2), strides: (1, 1))
var flatten = Flatten<Float>()
var linear = Dense<Float>(inputSize: 32, outputSize: 10)
@differentiable
func applied(to input: Tensor<Float>, in context: Context) -> Tensor<Float> {
// There isn't a "sequenced" defined with enough layers.
let intermediate = input.sequenced(
in: context,
through: reshapeToSquare, conv1, conv2, conv3, conv4)
return intermediate.sequenced(in: context, through: pool, flatten, linear)
}
}
let opt = SGD<CnnModelBN, Float>(learningRate: 0.4)
func modelInit() -> CnnModelBN { return CnnModelBN() }
let learner = Learner(data: data, lossFunction: softmaxCrossEntropy, optimizer: opt, initializingWith: modelInit)
let recorder = learner.makeDefaultDelegates(metrics: [accuracy])
learner.delegates.append(learner.makeNormalize(mean: mnistStats.mean, std: mnistStats.std))
time { try! learner.fit(1) }
Epoch 0: [0.103150696, 0.9708] 28583.478799 ms
TODO: hooks/LayerDelegates
More norms¶
Layer norm¶
From the paper: "batch normalization cannot be applied to online learning tasks or to extremely large distributed models where the minibatches have to be small".
General equation for a norm layer with learnable affine:
$$y = \frac{x - \mathrm{E}[x]}{ \sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \beta$$The difference with BatchNorm is
- we don't keep a moving average
- we don't average over the batches dimension but over the hidden dimension, so it's independent of the batch size
struct LayerNorm2D<Scalar: TensorFlowFloatingPoint>: Norm {
// Configuration hyperparameters
@noDerivative let epsilon: Scalar
// Trainable parameters
var scale: Tensor<Scalar>
var offset: Tensor<Scalar>
init(featureCount: Int, epsilon: Scalar = 1e-5) {
self.epsilon = epsilon
self.scale = Tensor(ones: [Int32(featureCount)])
self.offset = Tensor(zeros: [Int32(featureCount)])
}
@differentiable
func applied(to input: Tensor<Scalar>, in context: Context) -> Tensor<Scalar> {
let mean = input.mean(alongAxes: [1, 2, 3])
let variance = input.variance(alongAxes: [1, 2, 3])
let normalizer = rsqrt(variance + epsilon) * scale
return (input - mean) * normalizer + offset
}
}
struct ConvLN<Scalar: TensorFlowFloatingPoint>: Layer {
var conv: Conv2D<Scalar>
var norm: LayerNorm2D<Scalar>
init(
filterShape: (Int, Int, Int, Int),
strides: (Int, Int) = (1, 1),
padding: Padding = .valid,
activation: @escaping Conv2D<Scalar>.Activation = identity
) {
// TODO (when control flow AD works): use Conv2D without bias
self.conv = Conv2D(
filterShape: filterShape,
strides: strides,
padding: padding,
activation: activation)
self.norm = LayerNorm2D(featureCount: filterShape.3, epsilon: 1e-5)
}
@differentiable
func applied(to input: Tensor<Scalar>, in context: Context) -> Tensor<Scalar> {
return norm.applied(to: conv.applied(to: input, in: context), in: context)
}
}
struct CnnModelLN: Layer {
var reshapeToSquare = Reshape<Float>([-1, exampleSideSize, exampleSideSize, 1])
var conv1 = ConvLN<Float>(
filterShape: (5, 5, 1, 8),
strides: (2, 2),
padding: .same,
activation: relu)
var conv2 = ConvLN<Float>(
filterShape: (3, 3, 8, 16),
strides: (2, 2),
padding: .same,
activation: relu)
var conv3 = ConvLN<Float>(
filterShape: (3, 3, 16, 32),
strides: (2, 2),
padding: .same,
activation: relu)
var conv4 = ConvLN<Float>(
filterShape: (3, 3, 32, 32),
strides: (2, 2),
padding: .same,
activation: relu)
var pool = AvgPool2D<Float>(poolSize: (2, 2), strides: (1, 1))
var flatten = Flatten<Float>()
var linear = Dense<Float>(inputSize: 32, outputSize: Int(classCount))
@differentiable
func applied(to input: Tensor<Float>, in context: Context) -> Tensor<Float> {
// There isn't a "sequenced" defined with enough layers.
let intermediate = input.sequenced(
in: context,
through: reshapeToSquare, conv1, conv2, conv3, conv4)
return intermediate.sequenced(in: context, through: pool, flatten, linear)
}
}
let opt = SGD<CnnModel, Float>(learningRate: 0.4)
func modelInit() -> CnnModel { return CnnModel() }
let learner = Learner(data: data, lossFunction: softmaxCrossEntropy1, optimizer: opt, initializingWith: modelInit)
let recorder = learner.makeDefaultDelegates(metrics: [accuracy])
time { try! learner.fit(1) }
error: <Cell 19>:42:16: error: ambiguous use of 'learner'
let recorder = learner.makeDefaultDelegates(metrics: [accuracy])
^
<Cell 19>:41:5: note: 'learner' declared here
let learner = Learner(data: data, lossFunction: softmaxCrossEntropy1, optimizer: opt, initializingWith: modelInit)
^
error: <Cell 19>:41:49: error: use of unresolved identifier 'softmaxCrossEntropy1'; did you mean 'softmaxCrossEntropy'?
let learner = Learner(data: data, lossFunction: softmaxCrossEntropy1, optimizer: opt, initializingWith: modelInit)
^~~~~~~~~~~~~~~~~~~~
softmaxCrossEntropy
TensorFlow.softmaxCrossEntropy:2:13: note: 'softmaxCrossEntropy' declared here
public func softmaxCrossEntropy<Scalar>(logits: TensorFlow.Tensor<Scalar>, labels: TensorFlow.Tensor<Int32>) -> TensorFlow.Tensor<Scalar> where Scalar : TensorFlowFloatingPoint
^
TensorFlow.softmaxCrossEntropy:2:13: note: 'softmaxCrossEntropy' declared here
public func softmaxCrossEntropy<Scalar>(logits: TensorFlow.Tensor<Scalar>, probabilities: TensorFlow.Tensor<Scalar>) -> TensorFlow.Tensor<Scalar> where Scalar : TensorFlowFloatingPoint
^
error: <Cell 19>:27:62: error: use of unresolved identifier 'classCount'
var linear = Dense<Float>(inputSize: 32, outputSize: Int(classCount))
^~~~~~~~~~
error: <Cell 19>:2:47: error: use of unresolved identifier 'exampleSideSize'
var reshapeToSquare = Reshape<Float>([-1, exampleSideSize, exampleSideSize, 1])
^~~~~~~~~~~~~~~
error: <Cell 19>:2:64: error: use of unresolved identifier 'exampleSideSize'
var reshapeToSquare = Reshape<Float>([-1, exampleSideSize, exampleSideSize, 1])
^~~~~~~~~~~~~~~
error: <Cell 19>:40:48: error: missing argument for parameter 'sizeIn' in call
func modelInit() -> CnnModel { return CnnModel() }
^
sizeIn: <#Int#>
FastaiNotebook_06_cuda.CnnModel:10:12: note: 'init(sizeIn:channelIn:channelOut:nFilters:)' declared here
public init(sizeIn: Int, channelIn: Int, channelOut: Int, nFilters: [Int])
^
struct InstanceNorm<Scalar: TensorFlowFloatingPoint>: Norm {
// Configuration hyperparameters
@noDerivative let epsilon: Scalar
// Trainable parameters
var scale: Tensor<Scalar>
var offset: Tensor<Scalar>
init(featureCount: Int, epsilon: Scalar = 1e-5) {
self.epsilon = epsilon
self.scale = Tensor(ones: [Int32(featureCount)])
self.offset = Tensor(zeros: [Int32(featureCount)])
}
@differentiable
func applied(to input: Tensor<Scalar>, in context: Context) -> Tensor<Scalar> {
let mean = input.mean(alongAxes: [2, 3])
let variance = input.variance(alongAxes: [2, 3])
let normalizer = rsqrt(variance + epsilon) * scale
return (input - mean) * normalizer + offset
}
}
struct ConvIN<Scalar: TensorFlowFloatingPoint>: Layer {
var conv: Conv2D<Scalar>
var norm: InstanceNorm<Scalar>
init(
filterShape: (Int, Int, Int, Int),
strides: (Int, Int) = (1, 1),
padding: Padding = .valid,
activation: @escaping Conv2D<Scalar>.Activation = identity
) {
// TODO (when control flow AD works): use Conv2D without bias
self.conv = Conv2D(
filterShape: filterShape,
strides: strides,
padding: padding,
activation: activation)
self.norm = InstanceNorm(featureCount: filterShape.3, epsilon: 1e-5)
}
@differentiable
func applied(to input: Tensor<Scalar>, in context: Context) -> Tensor<Scalar> {
return norm.applied(to: conv.applied(to: input, in: context), in: context)
}
}
Lost in all those norms? The authors from the group norm paper have you covered:
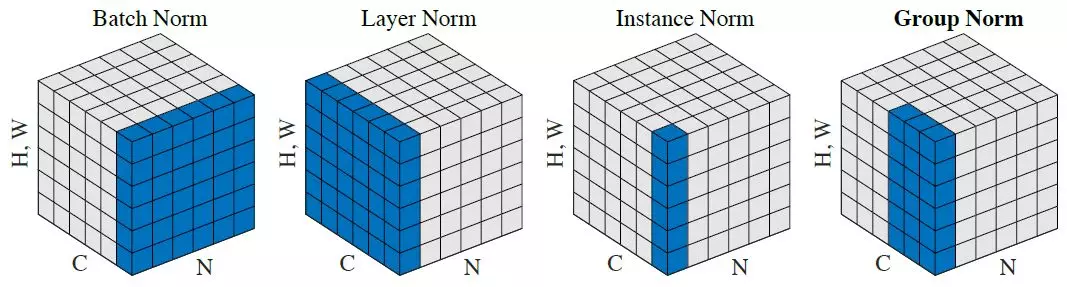
TODO/skipping GroupNorm
Running Batch Norm¶
struct RunningBatchNorm<Scalar: TensorFlowFloatingPoint>: LearningPhaseDependent, Norm {
// Configuration hyperparameters
@noDerivative let momentum: Scalar
@noDerivative let epsilon: Scalar
// Running statistics
@noDerivative let runningSum: Reference<Tensor<Scalar>>
@noDerivative let runningSumOfSquares: Reference<Tensor<Scalar>>
@noDerivative let runningCount: Reference<Scalar>
@noDerivative let samplesSeen: Reference<Int32>
// Trainable parameters
var scale: Tensor<Scalar>
var offset: Tensor<Scalar>
// TODO: check why these aren't being synthesized
typealias Input = Tensor<Scalar>
typealias Output = Tensor<Scalar>
init(featureCount: Int, momentum: Scalar, epsilon: Scalar = 1e-5) {
self.momentum = momentum
self.epsilon = epsilon
self.scale = Tensor(ones: [Int32(featureCount)])
self.offset = Tensor(zeros: [Int32(featureCount)])
self.runningSum = Reference(Tensor(0))
self.runningSumOfSquares = Reference(Tensor(0))
self.runningCount = Reference(Scalar(0))
self.samplesSeen = Reference(0)
}
init(featureCount: Int, epsilon: Scalar = 1e-5) {
self.init(featureCount: featureCount, momentum: 0.9, epsilon: epsilon)
}
@differentiable
func applyingTraining(to input: Tensor<Scalar>) -> Tensor<Scalar> {
let (batch, channels) = (input.shape[0], Scalar(input.shape[3]))
let sum = input.sum(alongAxes: [0, 1, 2])
let sumOfSquares = (input * input).sum(alongAxes: [0, 1, 2])
let count = Scalar(input.scalarCount).withoutDerivative() / channels
let mom = momentum / sqrt(Scalar(batch) - 1)
let runningSum = mom * self.runningSum.value + (1 - mom) * sum
let runningSumOfSquares = mom * self.runningSumOfSquares.value + (
1 - mom) * sumOfSquares
let runningCount = mom * self.runningCount.value + (1 - mom) * count
self.runningSum.value = runningSum
self.runningSumOfSquares.value = runningSumOfSquares
self.runningCount.value = runningCount
self.samplesSeen.value += batch
let mean = runningSum / runningCount
let variance = runningSumOfSquares / runningCount - mean * mean
let normalizer = rsqrt(variance + epsilon) * scale
return (input - mean) * normalizer + offset
}
@differentiable
func applyingInference(to input: Tensor<Scalar>) -> Tensor<Scalar> {
let mean = runningSum.value / runningCount.value
let variance = runningSumOfSquares.value / runningCount.value - mean * mean
let normalizer = rsqrt(variance + epsilon) * scale
return (input - mean) * normalizer + offset
}
}
TODO: XLA compilation + test RBN
Export¶
notebookToScript(fname: (Path.cwd / "07_batchnorm.ipynb").string)