#!/usr/bin/env python
# coding: utf-8
# # SGDR - Stochastic Gradient Descent with Warm Restarts
# In this tutorial we are going to be looking at the `SGDR` or as referred to in the `timm` library - the `cosine` scheduler in little more detail with all the supporting hyperparams.
# The SGDR schedule as mentioned in the [paper](https://arxiv.org/abs/1608.03983) looks like:
#  # In[1]:
#hide
get_ipython().run_line_magic('load_ext', 'autoreload')
get_ipython().run_line_magic('autoreload', '2')
# In[2]:
from timm.scheduler.cosine_lr import CosineLRScheduler
from nbdev.showdoc import show_doc
# In[3]:
show_doc(CosineLRScheduler)
# The `CosineLRScheduler` as shown above accepts an `optimizer` and also some hyperparams which we will look into in detail below. We will first see how we can train models using the `cosine` LR scheduler by first using `timm` training docs and then look at how we can use this scheduler as standalone scheduler for our custom training scripts.
# ## Using `cosine` scheduler with `timm` training script
# To train models using the `cosine` scheduler we simply update the training script args passed by passing in `--sched cosine` parameter alongside the necessary hyperparams. In this section we will also look at how each of the hyperparams update the `cosine` scheduler.
# > NOTE: In the paper this scheduler is referred to as `SGDR` but in `timm` this is referred to as `cosine` scheduler. They are both one and the same with minor implementation difference.
# The training command to use `cosine` scheduler looks something like:
#
# ```python
# python train.py ../imagenette2-320/ --sched cosine
# ```
# ## Args
# This way we start to use the `cosine` scheduler with all the defaults. Let's now look at the associated hyperparams and how that updates the annealing schedule.
# ### `optimizer`
# This is the `optimizer` that will be used for the training process.
# In[4]:
from timm import create_model
from timm.optim import create_optimizer
from types import SimpleNamespace
# In[5]:
model = create_model('resnet34')
args = SimpleNamespace()
args.weight_decay = 0
args.lr = 1e-4
args.opt = 'adam'
args.momentum = 0.9
optimizer = create_optimizer(args, model)
# This `optimizer` object created using `create_optimizer` is what get's passed to the `optimizer` argument.
# ### `t_initial`
# The initial number of epochs. Example, 50, 100 etc.
# ### `t_mul`
# Defaults to 1.0. Updates the `SGDR` schedule annealing.
#
# In[1]:
#hide
get_ipython().run_line_magic('load_ext', 'autoreload')
get_ipython().run_line_magic('autoreload', '2')
# In[2]:
from timm.scheduler.cosine_lr import CosineLRScheduler
from nbdev.showdoc import show_doc
# In[3]:
show_doc(CosineLRScheduler)
# The `CosineLRScheduler` as shown above accepts an `optimizer` and also some hyperparams which we will look into in detail below. We will first see how we can train models using the `cosine` LR scheduler by first using `timm` training docs and then look at how we can use this scheduler as standalone scheduler for our custom training scripts.
# ## Using `cosine` scheduler with `timm` training script
# To train models using the `cosine` scheduler we simply update the training script args passed by passing in `--sched cosine` parameter alongside the necessary hyperparams. In this section we will also look at how each of the hyperparams update the `cosine` scheduler.
# > NOTE: In the paper this scheduler is referred to as `SGDR` but in `timm` this is referred to as `cosine` scheduler. They are both one and the same with minor implementation difference.
# The training command to use `cosine` scheduler looks something like:
#
# ```python
# python train.py ../imagenette2-320/ --sched cosine
# ```
# ## Args
# This way we start to use the `cosine` scheduler with all the defaults. Let's now look at the associated hyperparams and how that updates the annealing schedule.
# ### `optimizer`
# This is the `optimizer` that will be used for the training process.
# In[4]:
from timm import create_model
from timm.optim import create_optimizer
from types import SimpleNamespace
# In[5]:
model = create_model('resnet34')
args = SimpleNamespace()
args.weight_decay = 0
args.lr = 1e-4
args.opt = 'adam'
args.momentum = 0.9
optimizer = create_optimizer(args, model)
# This `optimizer` object created using `create_optimizer` is what get's passed to the `optimizer` argument.
# ### `t_initial`
# The initial number of epochs. Example, 50, 100 etc.
# ### `t_mul`
# Defaults to 1.0. Updates the `SGDR` schedule annealing.
# 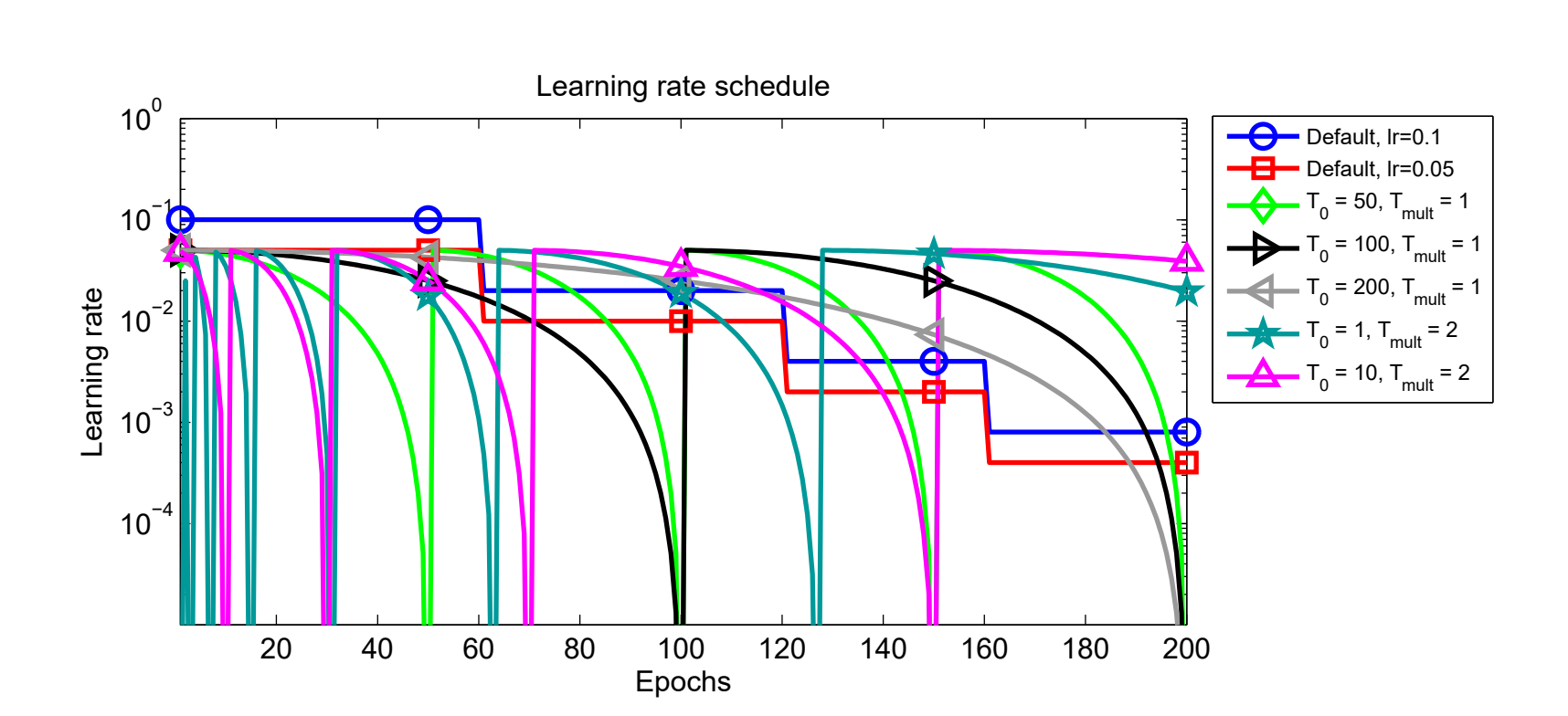 # As shown in the image below, here **T0** is the `t_initial` hyperparameter and **Tmult** is the `t_mul` hyperparameter. One can see how updating these parameters updates the scheduler.
# ### `lr_min`
# Defaults to `1e-5`. The minimum learning rate to use during the scheduling. The learning rate does not ever go below this value.
# ### `decay_rate`
# When `decay_rate` > 0 and <1., at every restart the learning rate is decayed by new learning rate which equals `lr * decay_rate`. So if `decay_rate=0.5`, then in that case, the new learning rate becomes half the initial `lr`.
# In[6]:
from matplotlib import pyplot as plt
def get_lr_per_epoch(scheduler, num_epoch):
lr_per_epoch = []
for epoch in range(num_epoch):
lr_per_epoch.append(scheduler.get_epoch_values(epoch))
return lr_per_epoch
# #### `decay_rate=1.` or no decay
# In[7]:
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, decay_rate=1., lr_min=1e-5)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch*2)
plt.plot([i for i in range(num_epoch*2)], lr_per_epoch);
# #### `decay_rate=0.5`
# In[8]:
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, decay_rate=0.5, lr_min=1e-5)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch*2)
plt.plot([i for i in range(num_epoch*2)], lr_per_epoch);
# ### `warmup_t`
# Defines the number of warmup epochs.
# ### `warmup_lr_init`
# The initial learning rate during warmup.
# In[9]:
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, warmup_t=5, warmup_lr_init=1e-5)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch)
plt.plot([i for i in range(num_epoch)], lr_per_epoch, label="With warmup");
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch)
plt.plot([i for i in range(num_epoch)], lr_per_epoch, label="Without warmup", alpha=0.8);
plt.legend();
# As we can see by setting up `warmup_t` and `warmup_lr_init`, the `cosine` scheduler first starts with a value of `warmup_lr_init`, then gradually progresses up to the `initial_lr` set in the optimizer which is 1e-4. It takes `warmup_t` number of epochs to go from `warmup_lr_init` to `initial_lr`.
# ### `warmup_prefix`
# Defaults to `False`. If set to `True`, then every new epoch number equals `epoch = epoch - warmup_t`.
# In[10]:
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, warmup_t=5, warmup_lr_init=1e-5)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch)
plt.plot([i for i in range(num_epoch)], lr_per_epoch, label="Without warmup_prefix");
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, warmup_t=5, warmup_lr_init=1e-5, warmup_prefix=True)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch)
plt.plot([i for i in range(num_epoch)], lr_per_epoch, label="With warmup_prefix");
plt.legend();
# In the example above we can see how the `warmup_prefix` updates the LR annealing schedule.
# ### `cycle_limit`
# The number of maximum restarts in SGDR.
# #### `cycle_limit=1`
# In[11]:
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, cycle_limit=1)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch*2)
plt.plot([i for i in range(num_epoch*2)], lr_per_epoch);
# #### `cycle_limit=2`
# In[12]:
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, cycle_limit=2)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch*2)
plt.plot([i for i in range(num_epoch*2)], lr_per_epoch);
# ### `t_in_epochs`
# If set to False, the learning rates returned for epoch `t` are `None`.
# In[13]:
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, t_in_epochs=False)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch)
lr_per_epoch[:5]
# ### `noise_range_t`
# Add noise to learning rate scheduler.
# ### `noise_pct`
# The amount of noise to be added. Defaults to 0.67.
# ### `noise_std`
# Noise standard deviation. Defaults to 1.0.
# ### `noise_seed`
# Noise seed to use. Defaults to 42.
# ### `initialize`
# If set to True, then, the an attributes `initial_lr` is set to each param group. Defaults to `True`.
# > NOTE: we leave it up to the reader to try and experiment how the LR annealing scheduling get's updated by adding in noise hyperparams.
# As shown in the image below, here **T0** is the `t_initial` hyperparameter and **Tmult** is the `t_mul` hyperparameter. One can see how updating these parameters updates the scheduler.
# ### `lr_min`
# Defaults to `1e-5`. The minimum learning rate to use during the scheduling. The learning rate does not ever go below this value.
# ### `decay_rate`
# When `decay_rate` > 0 and <1., at every restart the learning rate is decayed by new learning rate which equals `lr * decay_rate`. So if `decay_rate=0.5`, then in that case, the new learning rate becomes half the initial `lr`.
# In[6]:
from matplotlib import pyplot as plt
def get_lr_per_epoch(scheduler, num_epoch):
lr_per_epoch = []
for epoch in range(num_epoch):
lr_per_epoch.append(scheduler.get_epoch_values(epoch))
return lr_per_epoch
# #### `decay_rate=1.` or no decay
# In[7]:
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, decay_rate=1., lr_min=1e-5)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch*2)
plt.plot([i for i in range(num_epoch*2)], lr_per_epoch);
# #### `decay_rate=0.5`
# In[8]:
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, decay_rate=0.5, lr_min=1e-5)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch*2)
plt.plot([i for i in range(num_epoch*2)], lr_per_epoch);
# ### `warmup_t`
# Defines the number of warmup epochs.
# ### `warmup_lr_init`
# The initial learning rate during warmup.
# In[9]:
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, warmup_t=5, warmup_lr_init=1e-5)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch)
plt.plot([i for i in range(num_epoch)], lr_per_epoch, label="With warmup");
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch)
plt.plot([i for i in range(num_epoch)], lr_per_epoch, label="Without warmup", alpha=0.8);
plt.legend();
# As we can see by setting up `warmup_t` and `warmup_lr_init`, the `cosine` scheduler first starts with a value of `warmup_lr_init`, then gradually progresses up to the `initial_lr` set in the optimizer which is 1e-4. It takes `warmup_t` number of epochs to go from `warmup_lr_init` to `initial_lr`.
# ### `warmup_prefix`
# Defaults to `False`. If set to `True`, then every new epoch number equals `epoch = epoch - warmup_t`.
# In[10]:
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, warmup_t=5, warmup_lr_init=1e-5)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch)
plt.plot([i for i in range(num_epoch)], lr_per_epoch, label="Without warmup_prefix");
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, warmup_t=5, warmup_lr_init=1e-5, warmup_prefix=True)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch)
plt.plot([i for i in range(num_epoch)], lr_per_epoch, label="With warmup_prefix");
plt.legend();
# In the example above we can see how the `warmup_prefix` updates the LR annealing schedule.
# ### `cycle_limit`
# The number of maximum restarts in SGDR.
# #### `cycle_limit=1`
# In[11]:
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, cycle_limit=1)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch*2)
plt.plot([i for i in range(num_epoch*2)], lr_per_epoch);
# #### `cycle_limit=2`
# In[12]:
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, cycle_limit=2)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch*2)
plt.plot([i for i in range(num_epoch*2)], lr_per_epoch);
# ### `t_in_epochs`
# If set to False, the learning rates returned for epoch `t` are `None`.
# In[13]:
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, t_in_epochs=False)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch)
lr_per_epoch[:5]
# ### `noise_range_t`
# Add noise to learning rate scheduler.
# ### `noise_pct`
# The amount of noise to be added. Defaults to 0.67.
# ### `noise_std`
# Noise standard deviation. Defaults to 1.0.
# ### `noise_seed`
# Noise seed to use. Defaults to 42.
# ### `initialize`
# If set to True, then, the an attributes `initial_lr` is set to each param group. Defaults to `True`.
# > NOTE: we leave it up to the reader to try and experiment how the LR annealing scheduling get's updated by adding in noise hyperparams.
 # In[1]:
#hide
get_ipython().run_line_magic('load_ext', 'autoreload')
get_ipython().run_line_magic('autoreload', '2')
# In[2]:
from timm.scheduler.cosine_lr import CosineLRScheduler
from nbdev.showdoc import show_doc
# In[3]:
show_doc(CosineLRScheduler)
# The `CosineLRScheduler` as shown above accepts an `optimizer` and also some hyperparams which we will look into in detail below. We will first see how we can train models using the `cosine` LR scheduler by first using `timm` training docs and then look at how we can use this scheduler as standalone scheduler for our custom training scripts.
# ## Using `cosine` scheduler with `timm` training script
# To train models using the `cosine` scheduler we simply update the training script args passed by passing in `--sched cosine` parameter alongside the necessary hyperparams. In this section we will also look at how each of the hyperparams update the `cosine` scheduler.
# > NOTE: In the paper this scheduler is referred to as `SGDR` but in `timm` this is referred to as `cosine` scheduler. They are both one and the same with minor implementation difference.
# The training command to use `cosine` scheduler looks something like:
#
# ```python
# python train.py ../imagenette2-320/ --sched cosine
# ```
# ## Args
# This way we start to use the `cosine` scheduler with all the defaults. Let's now look at the associated hyperparams and how that updates the annealing schedule.
# ### `optimizer`
# This is the `optimizer` that will be used for the training process.
# In[4]:
from timm import create_model
from timm.optim import create_optimizer
from types import SimpleNamespace
# In[5]:
model = create_model('resnet34')
args = SimpleNamespace()
args.weight_decay = 0
args.lr = 1e-4
args.opt = 'adam'
args.momentum = 0.9
optimizer = create_optimizer(args, model)
# This `optimizer` object created using `create_optimizer` is what get's passed to the `optimizer` argument.
# ### `t_initial`
# The initial number of epochs. Example, 50, 100 etc.
# ### `t_mul`
# Defaults to 1.0. Updates the `SGDR` schedule annealing.
#
# In[1]:
#hide
get_ipython().run_line_magic('load_ext', 'autoreload')
get_ipython().run_line_magic('autoreload', '2')
# In[2]:
from timm.scheduler.cosine_lr import CosineLRScheduler
from nbdev.showdoc import show_doc
# In[3]:
show_doc(CosineLRScheduler)
# The `CosineLRScheduler` as shown above accepts an `optimizer` and also some hyperparams which we will look into in detail below. We will first see how we can train models using the `cosine` LR scheduler by first using `timm` training docs and then look at how we can use this scheduler as standalone scheduler for our custom training scripts.
# ## Using `cosine` scheduler with `timm` training script
# To train models using the `cosine` scheduler we simply update the training script args passed by passing in `--sched cosine` parameter alongside the necessary hyperparams. In this section we will also look at how each of the hyperparams update the `cosine` scheduler.
# > NOTE: In the paper this scheduler is referred to as `SGDR` but in `timm` this is referred to as `cosine` scheduler. They are both one and the same with minor implementation difference.
# The training command to use `cosine` scheduler looks something like:
#
# ```python
# python train.py ../imagenette2-320/ --sched cosine
# ```
# ## Args
# This way we start to use the `cosine` scheduler with all the defaults. Let's now look at the associated hyperparams and how that updates the annealing schedule.
# ### `optimizer`
# This is the `optimizer` that will be used for the training process.
# In[4]:
from timm import create_model
from timm.optim import create_optimizer
from types import SimpleNamespace
# In[5]:
model = create_model('resnet34')
args = SimpleNamespace()
args.weight_decay = 0
args.lr = 1e-4
args.opt = 'adam'
args.momentum = 0.9
optimizer = create_optimizer(args, model)
# This `optimizer` object created using `create_optimizer` is what get's passed to the `optimizer` argument.
# ### `t_initial`
# The initial number of epochs. Example, 50, 100 etc.
# ### `t_mul`
# Defaults to 1.0. Updates the `SGDR` schedule annealing.
#  # As shown in the image below, here **T0** is the `t_initial` hyperparameter and **Tmult** is the `t_mul` hyperparameter. One can see how updating these parameters updates the scheduler.
# ### `lr_min`
# Defaults to `1e-5`. The minimum learning rate to use during the scheduling. The learning rate does not ever go below this value.
# ### `decay_rate`
# When `decay_rate` > 0 and <1., at every restart the learning rate is decayed by new learning rate which equals `lr * decay_rate`. So if `decay_rate=0.5`, then in that case, the new learning rate becomes half the initial `lr`.
# In[6]:
from matplotlib import pyplot as plt
def get_lr_per_epoch(scheduler, num_epoch):
lr_per_epoch = []
for epoch in range(num_epoch):
lr_per_epoch.append(scheduler.get_epoch_values(epoch))
return lr_per_epoch
# #### `decay_rate=1.` or no decay
# In[7]:
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, decay_rate=1., lr_min=1e-5)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch*2)
plt.plot([i for i in range(num_epoch*2)], lr_per_epoch);
# #### `decay_rate=0.5`
# In[8]:
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, decay_rate=0.5, lr_min=1e-5)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch*2)
plt.plot([i for i in range(num_epoch*2)], lr_per_epoch);
# ### `warmup_t`
# Defines the number of warmup epochs.
# ### `warmup_lr_init`
# The initial learning rate during warmup.
# In[9]:
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, warmup_t=5, warmup_lr_init=1e-5)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch)
plt.plot([i for i in range(num_epoch)], lr_per_epoch, label="With warmup");
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch)
plt.plot([i for i in range(num_epoch)], lr_per_epoch, label="Without warmup", alpha=0.8);
plt.legend();
# As we can see by setting up `warmup_t` and `warmup_lr_init`, the `cosine` scheduler first starts with a value of `warmup_lr_init`, then gradually progresses up to the `initial_lr` set in the optimizer which is 1e-4. It takes `warmup_t` number of epochs to go from `warmup_lr_init` to `initial_lr`.
# ### `warmup_prefix`
# Defaults to `False`. If set to `True`, then every new epoch number equals `epoch = epoch - warmup_t`.
# In[10]:
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, warmup_t=5, warmup_lr_init=1e-5)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch)
plt.plot([i for i in range(num_epoch)], lr_per_epoch, label="Without warmup_prefix");
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, warmup_t=5, warmup_lr_init=1e-5, warmup_prefix=True)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch)
plt.plot([i for i in range(num_epoch)], lr_per_epoch, label="With warmup_prefix");
plt.legend();
# In the example above we can see how the `warmup_prefix` updates the LR annealing schedule.
# ### `cycle_limit`
# The number of maximum restarts in SGDR.
# #### `cycle_limit=1`
# In[11]:
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, cycle_limit=1)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch*2)
plt.plot([i for i in range(num_epoch*2)], lr_per_epoch);
# #### `cycle_limit=2`
# In[12]:
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, cycle_limit=2)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch*2)
plt.plot([i for i in range(num_epoch*2)], lr_per_epoch);
# ### `t_in_epochs`
# If set to False, the learning rates returned for epoch `t` are `None`.
# In[13]:
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, t_in_epochs=False)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch)
lr_per_epoch[:5]
# ### `noise_range_t`
# Add noise to learning rate scheduler.
# ### `noise_pct`
# The amount of noise to be added. Defaults to 0.67.
# ### `noise_std`
# Noise standard deviation. Defaults to 1.0.
# ### `noise_seed`
# Noise seed to use. Defaults to 42.
# ### `initialize`
# If set to True, then, the an attributes `initial_lr` is set to each param group. Defaults to `True`.
# > NOTE: we leave it up to the reader to try and experiment how the LR annealing scheduling get's updated by adding in noise hyperparams.
# As shown in the image below, here **T0** is the `t_initial` hyperparameter and **Tmult** is the `t_mul` hyperparameter. One can see how updating these parameters updates the scheduler.
# ### `lr_min`
# Defaults to `1e-5`. The minimum learning rate to use during the scheduling. The learning rate does not ever go below this value.
# ### `decay_rate`
# When `decay_rate` > 0 and <1., at every restart the learning rate is decayed by new learning rate which equals `lr * decay_rate`. So if `decay_rate=0.5`, then in that case, the new learning rate becomes half the initial `lr`.
# In[6]:
from matplotlib import pyplot as plt
def get_lr_per_epoch(scheduler, num_epoch):
lr_per_epoch = []
for epoch in range(num_epoch):
lr_per_epoch.append(scheduler.get_epoch_values(epoch))
return lr_per_epoch
# #### `decay_rate=1.` or no decay
# In[7]:
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, decay_rate=1., lr_min=1e-5)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch*2)
plt.plot([i for i in range(num_epoch*2)], lr_per_epoch);
# #### `decay_rate=0.5`
# In[8]:
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, decay_rate=0.5, lr_min=1e-5)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch*2)
plt.plot([i for i in range(num_epoch*2)], lr_per_epoch);
# ### `warmup_t`
# Defines the number of warmup epochs.
# ### `warmup_lr_init`
# The initial learning rate during warmup.
# In[9]:
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, warmup_t=5, warmup_lr_init=1e-5)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch)
plt.plot([i for i in range(num_epoch)], lr_per_epoch, label="With warmup");
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch)
plt.plot([i for i in range(num_epoch)], lr_per_epoch, label="Without warmup", alpha=0.8);
plt.legend();
# As we can see by setting up `warmup_t` and `warmup_lr_init`, the `cosine` scheduler first starts with a value of `warmup_lr_init`, then gradually progresses up to the `initial_lr` set in the optimizer which is 1e-4. It takes `warmup_t` number of epochs to go from `warmup_lr_init` to `initial_lr`.
# ### `warmup_prefix`
# Defaults to `False`. If set to `True`, then every new epoch number equals `epoch = epoch - warmup_t`.
# In[10]:
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, warmup_t=5, warmup_lr_init=1e-5)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch)
plt.plot([i for i in range(num_epoch)], lr_per_epoch, label="Without warmup_prefix");
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, warmup_t=5, warmup_lr_init=1e-5, warmup_prefix=True)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch)
plt.plot([i for i in range(num_epoch)], lr_per_epoch, label="With warmup_prefix");
plt.legend();
# In the example above we can see how the `warmup_prefix` updates the LR annealing schedule.
# ### `cycle_limit`
# The number of maximum restarts in SGDR.
# #### `cycle_limit=1`
# In[11]:
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, cycle_limit=1)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch*2)
plt.plot([i for i in range(num_epoch*2)], lr_per_epoch);
# #### `cycle_limit=2`
# In[12]:
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, cycle_limit=2)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch*2)
plt.plot([i for i in range(num_epoch*2)], lr_per_epoch);
# ### `t_in_epochs`
# If set to False, the learning rates returned for epoch `t` are `None`.
# In[13]:
num_epoch = 50
scheduler = CosineLRScheduler(optimizer, t_initial=num_epoch, t_in_epochs=False)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch)
lr_per_epoch[:5]
# ### `noise_range_t`
# Add noise to learning rate scheduler.
# ### `noise_pct`
# The amount of noise to be added. Defaults to 0.67.
# ### `noise_std`
# Noise standard deviation. Defaults to 1.0.
# ### `noise_seed`
# Noise seed to use. Defaults to 42.
# ### `initialize`
# If set to True, then, the an attributes `initial_lr` is set to each param group. Defaults to `True`.
# > NOTE: we leave it up to the reader to try and experiment how the LR annealing scheduling get's updated by adding in noise hyperparams.